# Long Short Term Memory

# Simple RNN

$y(t)=f(X(t)*W +y(t-1)*V+b)$

无隐藏层的循环神经网络，每个时刻的决策都依赖上一个时刻的决策结果。
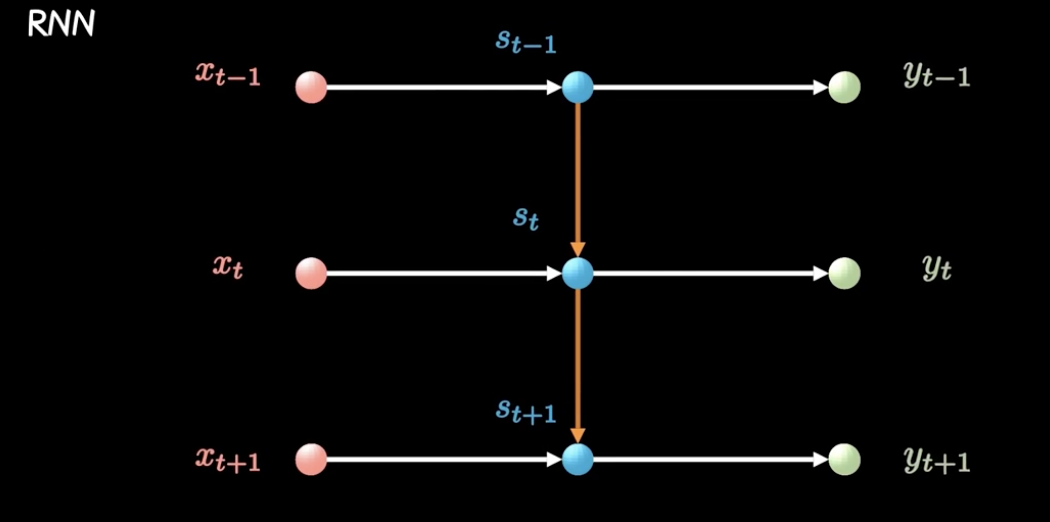
但是，新的知识不是直接加上上一时刻的知识，而是加上一个通过隐藏层后更加模糊宏观的知识，将这个定义为神经网络中的隐节点 $h$ ，也就是说，潜意识里直接利用的是一段记忆融合后的东西 $h$ ，而不单单是上一时间点的输出，这种加入隐藏层的RNN就是经典的RNN，如下图所示

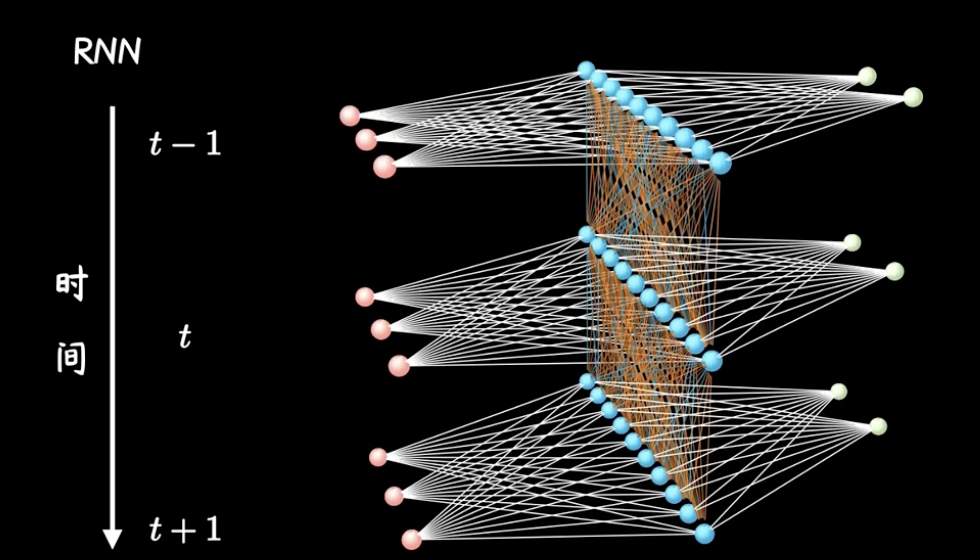
但是，存在隐藏层的RNN，由于误差反向传播，梯度会容易发生指数级别的衰减或者放大

因此RNN的记忆单元是短时的

# LSTM—长短期记忆

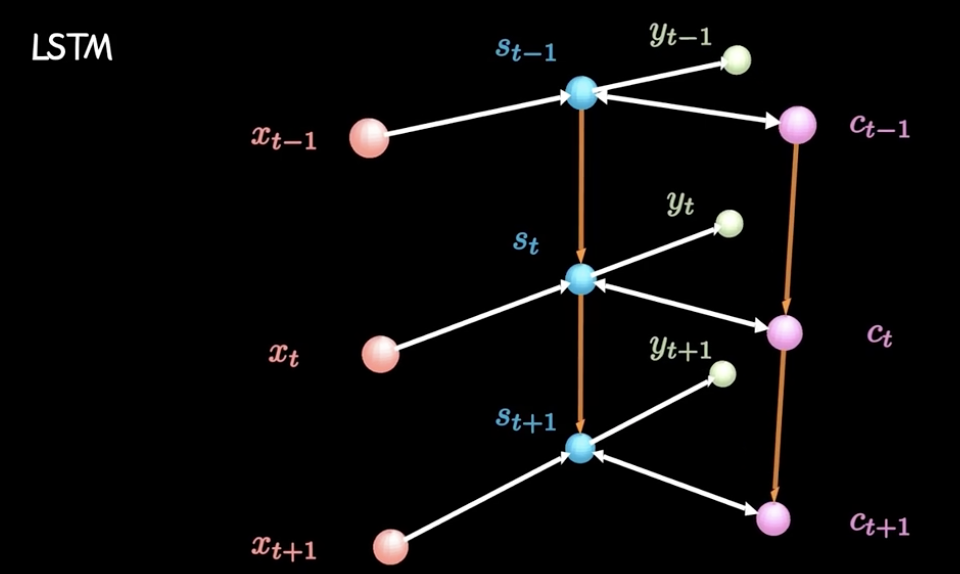
# 整体架构

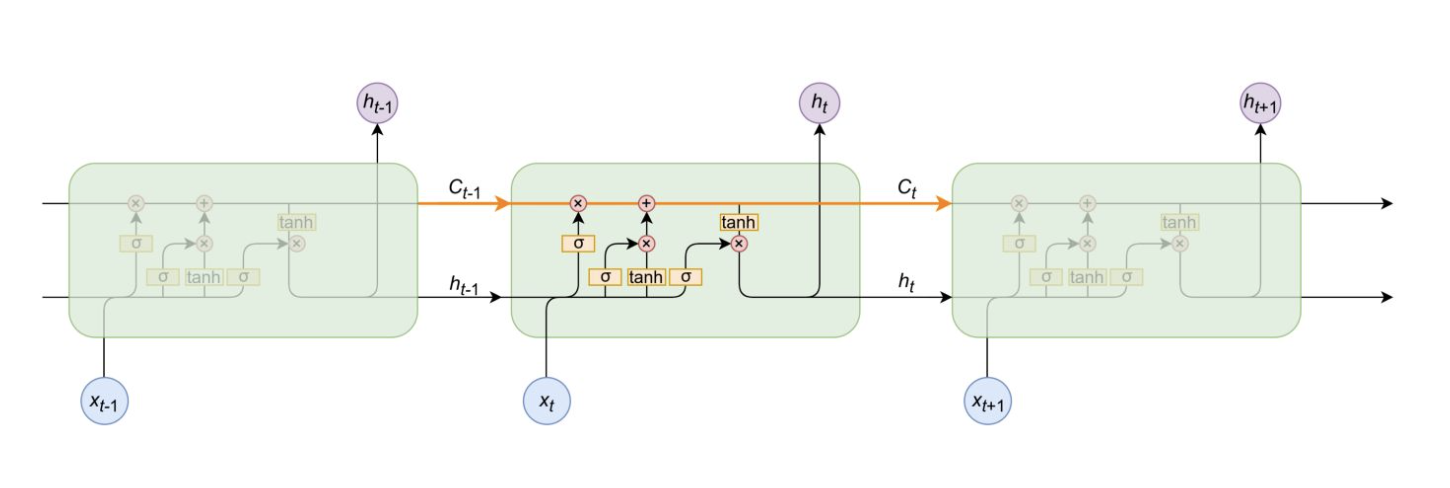
lstm引入了长短期记忆模块来解决RNN梯度消失或者爆炸问题，主要包括遗忘门、输入门、输出门

实际上是在RNN的基础上加了一个“日记本”，即长期记忆 $c$

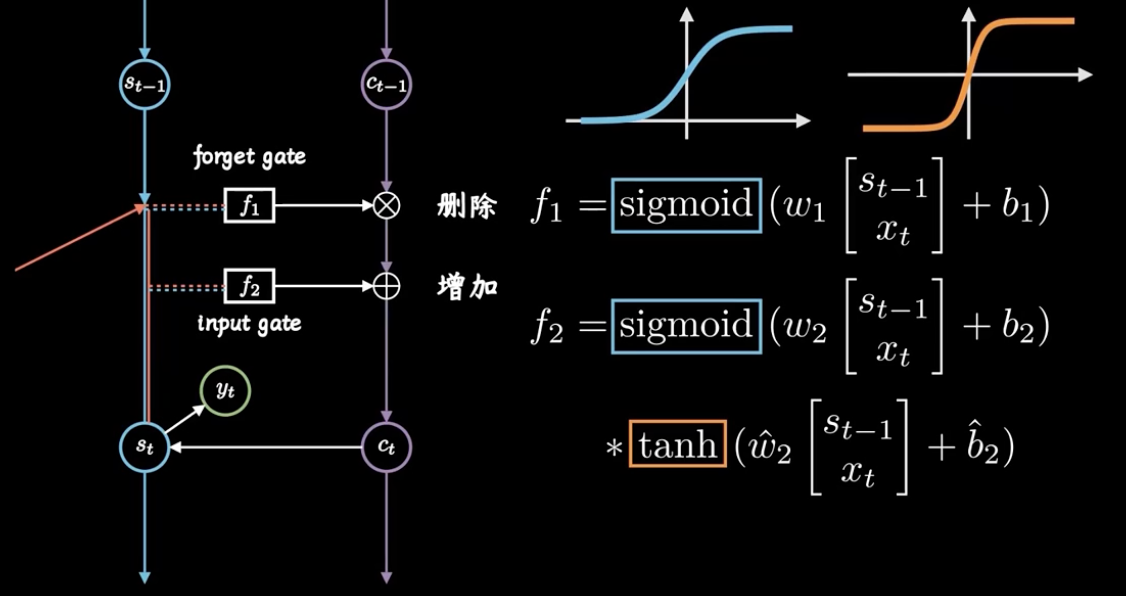
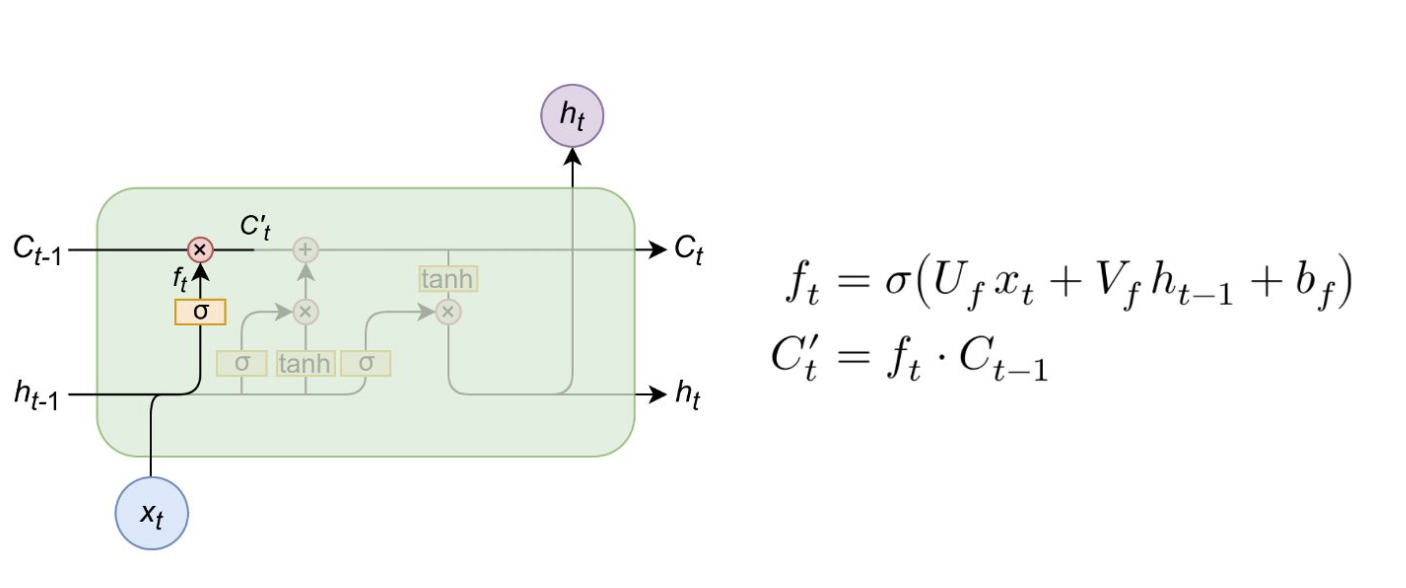
# 遗忘门

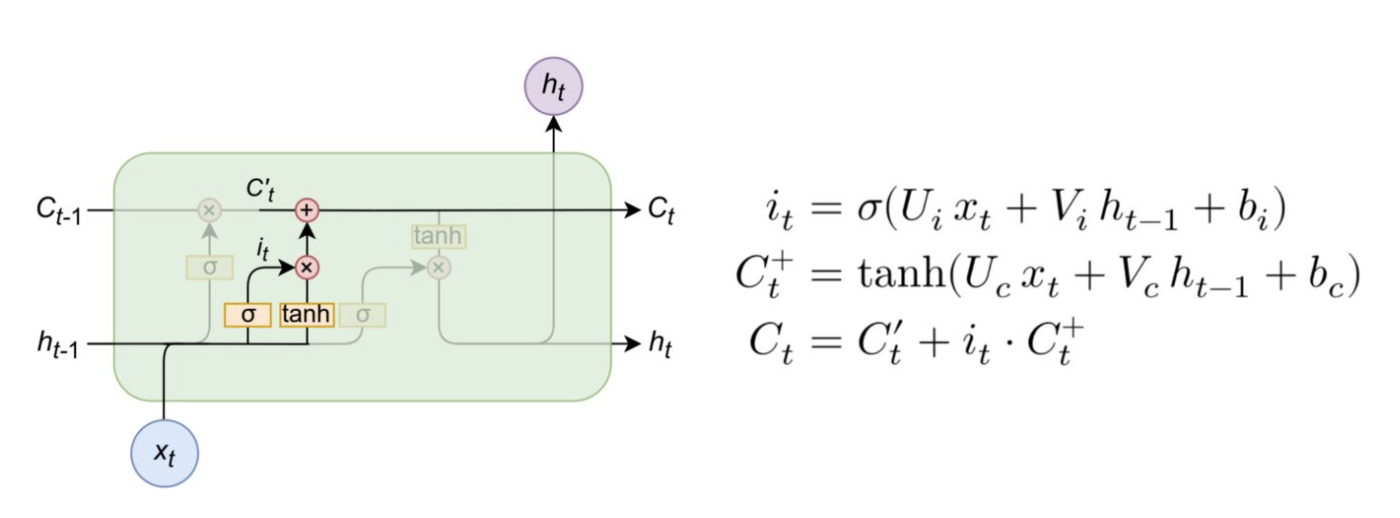
遗忘门将输入信息和隐藏层信息整合，然后结合整合后的信息对长期记忆中的信息选择性遗忘；

# 输入门

输入门利用整合后的信息选择性得写入信息到长期记忆中；

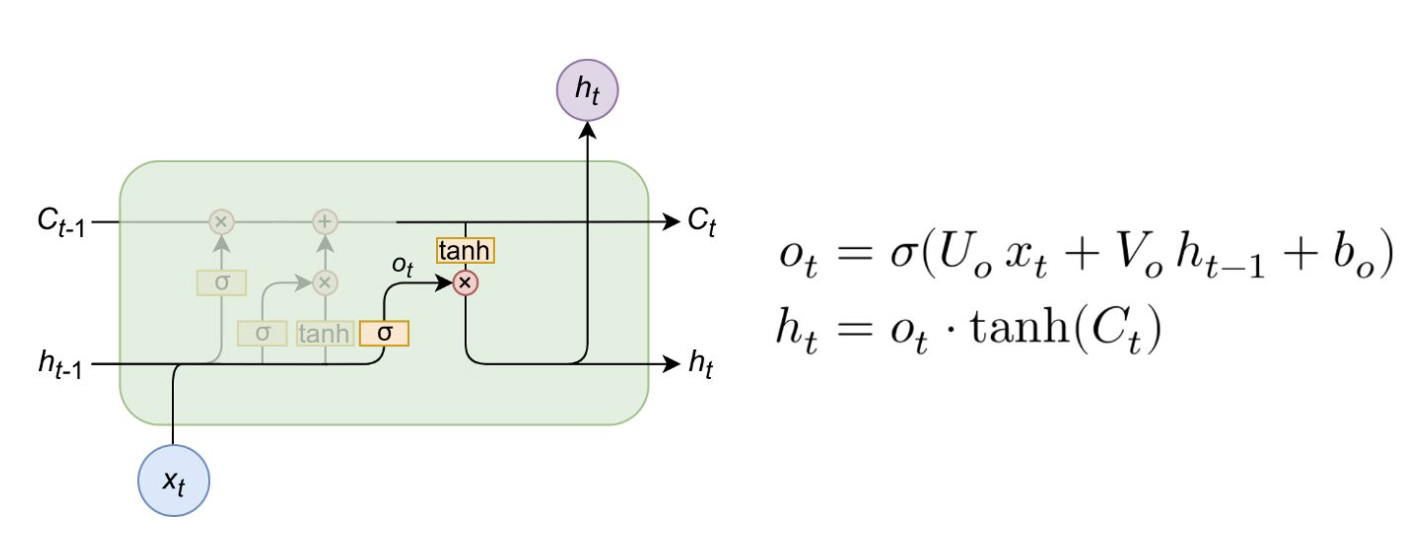
# 输出门

输出门结合长期和短期记忆，输出最终结果

# 公式

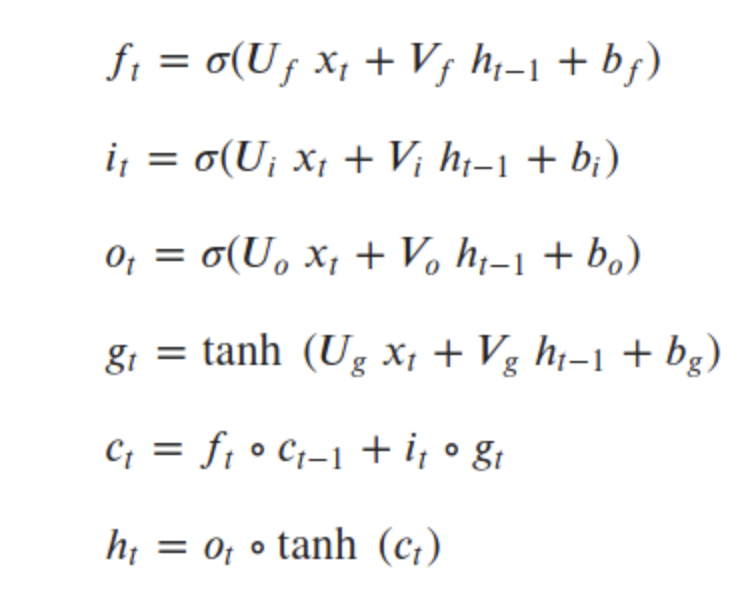
# 代码

class LSTM(nn.Module):

    def __init__(self, input_size, hidden_size):
        super(LSTM, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size

				# 输入门
        self.U_i = nn.Linear(self.input_size, self.hidden_size)
        self.V_i = nn.Linear(self.hidden_size, self.hidden_size)

        # 遗忘门
        self.U_f = nn.Linear(self.input_size, self.hidden_size)
        self.V_f = nn.Linear(self.hidden_size, self.hidden_size)

        # 长期记忆
        self.U_c = nn.Linear(self.input_size, self.hidden_size)
        self.V_c = nn.Linear(self.hidden_size, self.hidden_size)

        # 输出门
        self.U_o = nn.Linear(self.input_size, self.hidden_size)
        self.V_o = nn.Linear(self.hidden_size, self.hidden_size)

    def forward(self, x, init_states=None):
        batch_size, seq_len, n_dim = x.size()
        hidden_state = []
        if init_states is None:
            h_t, c_t = (
                torch.zeros(batch_size, self.hidden_size),
                torch.zeros(batch_size, self.hidden_size)
            )
        else:
            h_t, c_t = init_states

        for t in range(seq_len):
            x_t = x[:, t, :]            # 每时刻输入为当前的单词
            i_t = torch.sigmoid(self.U_i(x_t) + self.V_i(h_t))
            f_t = torch.sigmoid(self.U_f(x_t) + self.V_f(h_t))
            g_t = torch.tanh(self.U_c(x_t) + self.V_c(h_t))
            o_t = torch.sigmoid(self.U_o(x_t) + self.V_o(h_t))
            c_t = f_t * c_t + i_t * g_t
            h_t = o_t * torch.tanh(c_t)

            hidden_state.append(h_t.unsqueeze(0))
        hidden_state = torch.cat(hidden_state, dim=0)
        hidden_state = hidden_state.transpose(0, 1).contiguous()
        return hidden_state, (h_t, c_t)

# 注意

LSTM按时间维度展开，实际上是3维模型

2. LSTM的时间长度是输入数据的长度，即时间步（从代码可以看出）

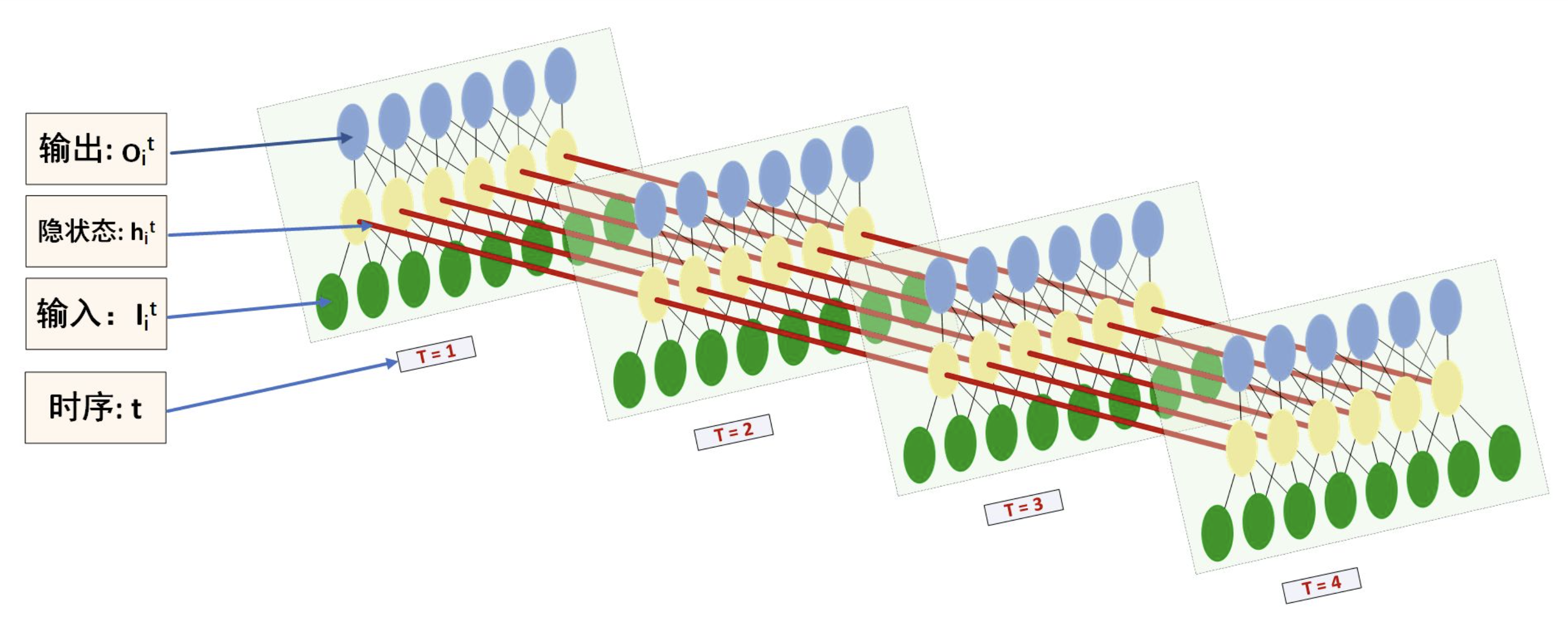
每个时间步，输入为当时的单个字符（从代码可以看出），之前的信息都在长期记忆中
上图为1个LSTMCell，只是把时间步展开了
整个计算过程如下图

← 数据增强——Embedding Mixup